LA HIPÉRBOLA
LA HIPÉRBOLA
¿Qué es una hipérbola?
La hipérbola es el conjunto de puntos del plano tales que el valor absoluto de la diferencia entre las distancias a dos puntos fijos, llamados focos, permanece constante. Dicho conjunto de puntos forma la curva con dos ramas que se observa en la figura 1.
Allí se muestra un punto P(x,y), los focos F1 y F2 separados una distancia igual a 2c. La forma matemática de expresar esta relación es a través de:
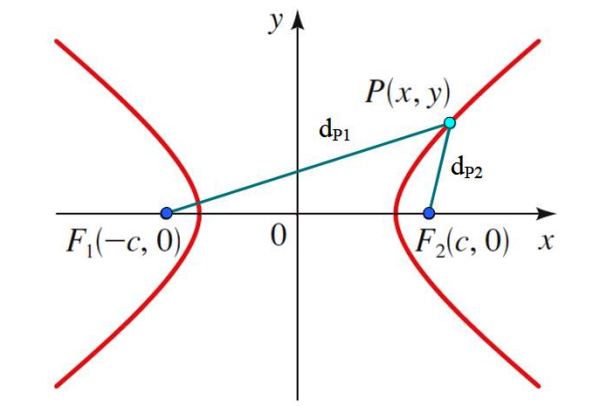
Todos los puntos de la hipérbola satisfacen esta condición, la cual conduce a la ecuación de la hipérbola, como se verá más adelante. Al punto medio entre los focos se le llama el centro C y en la figura coincide con el punto (0,0), pero la hipérbola también puede estar desplazada y su centro corresponder a otro punto de coordenadas C (h,k).
En la figura superior, el eje x es el eje focal de la hipérbola, ya que allí se encuentran los focos, pero se puede construir también una cuyo eje focal sea el eje y.
La hipérbola forma parte de las curvas conocidas como cónicas, que se llaman así porque pueden derivarse del corte de un cono con una sección plana. Se obtiene una hipérbola al intersectar el cono y el plano, siempre que este no pase por el vértice del cono y el ángulo que forme el plano con el eje del cono sea menor que el que forma con el eje generatriz del mismo.
Junto con la parábola, la circunferencia y la elipse, las cónicas son conocidas desde la antigüedad. El matemático griego Apolonio de Perga (262-190 aC) escribió un tratado de geometría donde detallaba sus propiedades y él mismo les dio los nombres con los que se conocen hasta hoy.
Características de la hipérbola
Estas son algunas de las características más resaltantes de una hipérbola:
- Es una curva plana, por lo tanto basta con dar las coordenadas (x,y) de cada punto que le pertenece.
- También es una curva abierta, a diferencia de la circunferencia o de la elipse.
- Tiene dos ramas dispuestas simétricamente.
- Tanto el eje vertical como el eje horizontal pueden ser considerados como ejes de simetría, pero el eje donde se ubican los focos se denomina eje focal o eje principal.
- Es simétrica respecto a su centro.
- La hipérbola intersecta al eje focal en dos puntos llamados vértices, por eso al eje focal se le denomina a veces eje real, mientras que al otro eje se le llama eje imaginario, porque no tiene puntos en común con la hipérbola.
- El centro de la hipérbola está ubicado a mitad de camino entre los puntos llamados focos.
- Está asociada con dos rectas muy particulares llamadas asíntotas, que son líneas a las cuales la hipérbola se aproxima, pero sin cruzarlas, cuando los valores de x e y son muy grandes. Las asíntotas se intersectan en el centro de la hipérbola.
Ecuaciones y fórmulas
Ecuación de la hipérbola con centro en (0,0)
Partiendo de la definición dada al comienzo:
A esta constante positiva, se la suele llamar 2a y es la distancia que separa los vértices de la hipérbola, entonces:
Por otra parte, dP1, dP2 y 2c son los lados del triángulo que se muestra en la figura 1, y por geometría elemental, la resta de los cuadrados de los lados de cualquier triángulo siempre es menor que el cuadrado del lado restante. Entonces:
4a2 < 4c2
Y:
a < c
Este resultado será útil en breve.
Como la distancia entre dos puntos P1(x1,y1) y P2(x2,y2) es:
Al sustituir las coordenadas P(x,y), F1(-c,0) y F2(c,0) queda:
Que equivale a:
Elevando al cuadrado en ambos miembros para eliminar las raíces y reorganizando los términos se llega a:
A la cantidad c2 – a2, que siempre es una cantidad positiva porque a < c, se la denomina b2, por lo tanto lo anterior se reescribe como:
2x2 – a2y2 = a2 b2
Dividiendo todos los términos por a2 b2, resulta la ecuación de la hipérbola centrada en (0,0) con el eje real horizontal:
Con a y b mayores que 0. A esta ecuación se le denomina ecuación canónica de la hipérbola y el denominador a2 siempre corresponde a la fracción positiva.
La hipérbola centrada en (0,0) y con el eje real vertical toma la forma:
Las intersecciones de la hipérbola con los ejes coordenados se encuentra haciendo respectivamente y = 0 y x = 0 en la ecuación:
Para y = 0
x2 /a2 = 1 ⇒ x2 = a2
x = ± a
La hipérbola corta al eje x en dos puntos llamados vértices, cuyas respectivas coordenadas x son: x = a y x = -a
Para x = 0
Se obtiene -y2 /b2 = 1, que no tiene solución real y se deduce que la hipérbola no corta al eje vertical.
Ecuación de la hipérbola con centro en (h,k)
Si el centro de la hipérbola se encuentra en el punto C(h,k), entonces su ecuación canónica es:
Elementos de la hipérbola
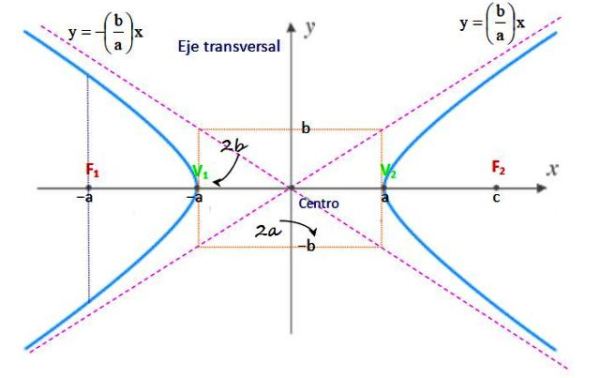
Centro
Es el punto medio del segmento F1F2 y sus coordenadas son (h,k) o (xo,yo).
Focos
Son los dos puntos fijos F1 y F2 que se encuentran sobre el eje real de la hipérbola, respecto de los cuales la diferencia de distancias al punto P(x,y) permanece constante. La distancia entre los focos y el centro de la hipérbola es “c”.
Radio vector
Se denomina así a la distancia entre un punto P y uno de los focos.
Distancia focal
Es la distancia que separa a ambos focos y equivale a 2c.
Vértices
Los vértices V1 y V2 son los puntos donde la hipérbola intersecta al eje real. Un vértice y el centro de la hipérbola se encuentran separados por la distancia a, por lo tanto, la distancia entre los vértices es 2a.
Eje focal, eje principal o eje real
Es el eje donde se ubican los focos y mide 2c. Puede estar ubicado sobre cualquiera de los dos ejes cartesianos y la hipérbola lo intersecta en los puntos llamados vértices.
Eje transversal, eje secundario o eje imaginario
Es el eje perpendicular al eje focal y mide 2b. La hipérbola no lo intersecta, por ello se le llama también eje imaginario.
Asíntotas
Son dos rectas, cuyas respectivas pendientes son m1 = (b/a) y m2 = − (b/a), las cuales se cruzan en el centro de la hipérbola. La curva nunca intersecta estas rectas y el producto entre las distancias de un punto cualquiera de la hipérbola a las asíntotas, es constante.
Para encontrar las ecuaciones de las asíntotas, basta con igualar el lado izquierdo de la ecuación canónica de la hipérbola a 0. Por ejemplo, para la hipérbola centrada en el origen:
Rectángulo de la hipérbola
Es el rectángulo cuyo ancho es la distancia entre los vértices 2a y la distancia 2b y está centrado en el centro de la hipérbola. Su construcción facilita el trazado manual de la hipérbola.
Lado recto
Cuerda que pasa por uno de los focos, perpendicularmente al eje real.
Excentricidad
Se define como el cociente entre la distancia focal y el eje real:
e = c/a
Siempre es mayor que 1, ya que c es mayor que a, y menor que √2.
El valor de e indica si la hipérbola es más bien cerrada (rectángulo estrecho, alargado en dirección al eje principal) o abierta (rectángulo ancho, alargado en dirección al eje imaginario).
Recta tangente a la hipérbola en el punto P(x1,y1)
Una recta tangente a la hipérbola en un punto P(x1,y1) de la misma es la bisectriz de los dos radios vectores de dicho punto.
Para una hipérbola con el eje principal paralelo al eje x, la pendiente de la recta tangente a la hipérbola en un punto P(x1,y1) viene dada por:
Y si la hipérbola es de eje principal paralelo al eje y, entonces:
Ejemplos de hipérbola
Dispersión de partículas alfa por un núcleo
Al bombardear núcleos atómicos con partículas alfa, que no son otra cosa sino núcleos de helio, estos son repelidos, ya que cualquier núcleo atómico tiene carga positiva. Estos núcleos de helio se dispersan siguiendo trayectorias hiperbólicas.
Trayectorias de los cuerpos del sistema solar
En el sistema solar, los objetos se mueven bajo la acción de la fuerza de la gravedad. La descripción del movimiento se deriva de una ecuación diferencial en la cual la fuerza es conservativa e inversamente proporcional al cuadrado de la distancia. Y las soluciones de dicha ecuación son las posibles trayectorias que siguen los objetos.
Pues bien, estas trayectorias siempre son cónicas: circunferencias, elipses, parábolas o hipérbolas. Las dos primeras son curvas cerradas, y así es como se mueven los planetas, pero algunos cometas siguen trayectorias abiertas, como parábolas o hipérbolas, con el Sol ubicado en uno de los focos.
Mínimos de sonido
Cuando se tienen dos fuentes sonoras, como dos altavoces que emiten sonidos uniformemente en todas las direcciones, ubicados a lo largo de una línea recta, los mínimos de intensidad sonora (interferencia destructiva) se encuentran sobre una hipérbola cuyo eje principal es dicha línea, y en los focos de la hipérbola están los altavoces.
Ejercicio resuelto
Encontrar los elementos de la siguiente hipérbola: vértices, focos y asíntotas de la hipérbola y construir su gráfica:
Solución
El centro de esta hipérbola coincide con el origen de las coordenadas y su eje real es horizontal, ya que la fracción positiva corresponde a la variable x.
Los semiejes de la hipérbola son:
a2 = 16 ⇒ a = 4
b2 = 4 ⇒ b = 2
De esta manera, el rectángulo central mide 4 unidades de ancho y 2 unidades de alto. Recordando que más arriba se mencionó que c2 – a2 = b2 , entonces:
c2 = a2 + b2 ⇒ c2 = 16 + 4 = 20
Por lo tanto, la semi-distancia focal es:
c = √20 = 2√5
Y los focos están en los puntos de coordenadas F1 (-2√5,0) y F2 (2√5,0).
Las pendientes de las asíntotas son:
m = ±(b/a) = ±(2/4)=±0.5
Por lo tanto las ecuaciones respectivas de cada una son:
y1 = 0.5x ; y2 = -0.5x
La hipérbola se puede graficar fácilmente a través de un software en línea como Geogebra:
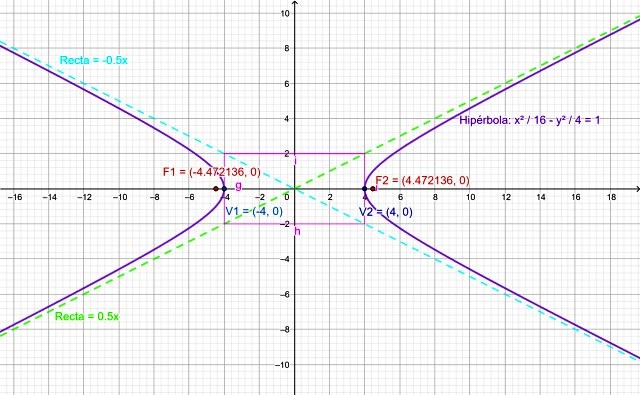

Comentarios
Publicar un comentario